返馳式轉換器之等效集總電容分析
摘要
返馳式轉換器運行在不連續導通模式(discontinuous conduction mode;DCM)時,量測功率開關汲-源極兩端電壓的低頻振鈴(ringing)之頻率,可推算出系統的等效集總電容。然而,此作法並無法確切掌握等效集總電容之組成元素,故難以改善等效集總電容,特別是如主動箝位返馳式轉換器(active clamp flyback converter)及準諧振返馳式轉換器(quasi-resonant flyback converter)等應用中,為減少開關功耗(switching loss)以提升效率,常需較精準的電容值以實現軟開關(soft switching)或波谷切換(valley switching)。因此,本文藉由分析變壓器與半導體元件的寄生電容特性,並透過實際量測元件特性,用以分析返馳式轉換器的等效集總電容,最後利用SIMPLIS 電路模擬軟體模擬、並與實測平台量測之結果相互驗證,掌握系統等效集總電容的組成,有助於達成高效率返馳式轉換器之設計。
前言
返馳式轉換器的等效集總電容是為功率開關汲極對初級側交流地的等效電容。圖1為返馳式轉換器之電路示意圖,其中CB為輸入端之大電容,Co為輸出電容,Q為功率開關,Do為輸出二極體,T為變壓器,n為匝數比,Lm為激磁電感(magnetizing inductance),Lk為漏電感(leakage inductance)。在功率開關斷開時,功率開關的電壓會因系統的等效集總電容分別與變壓器的激磁電感和漏電感引起低頻與高頻振鈴(ringing),如圖2。欲獲得系統的等效集總電容,一般量測功率開關的汲-源極兩端電壓的低頻振鈴之頻率,藉此推算系統的等效集總電容,但此方法並無法得知系統的等效集總電容之組成,雖然許多文獻均表示等效集總電容約略為功率開關的輸出電容,但實際上磁性元件(如:變壓器)與半導體元件中仍存在許多不能忽略的寄生電容。
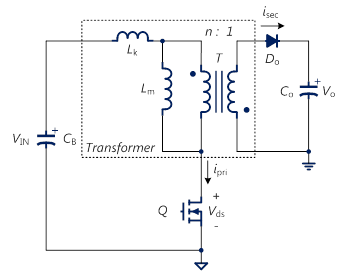
圖1 返馳式轉換器的電路示意圖
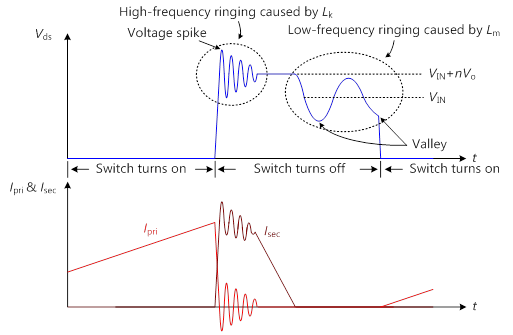
圖2 返馳式轉換器操作在不連續導通模式的電壓與電流波形
圖3所示為圖1之返馳式轉換器加上所有主要元件的寄生電容,其中Cp為變壓器初級側的分佈電容,Cs為變壓器次級側的分佈電容,Cps為變壓器初級側至次級側的級間(interwinding)電容,Cds 為功率開關的汲-源極電容,Cj_Do為輸出二極體的接面電容。
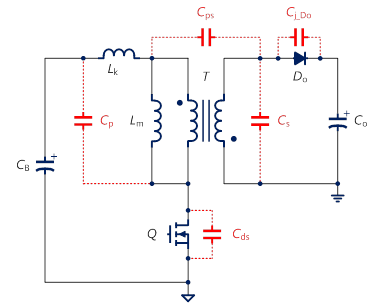
圖3 返馳式轉換器與寄生電容的示意圖
然而,系統的等效集總電容在某些電路架構中則是扮演了重要的角色,如準諧振返馳式轉換器,其轉換器的特點為轉換器將運作於不連續導通模式(DCM),當功率開關與輸出二極體均為斷開時,其功率開關的汲-源極兩端電壓將振鈴電壓之低點(亦稱為波谷電壓)時,將功率開關導通,即所謂的「波谷切換」,如圖2所示。此低頻振鈴為變壓器之激磁電感與系統的等效集總電容所引起,所以了解系統的等效集總電容,即可精準的達成波谷切換,進而降低開關轉換器的開關功耗。另於具軟開關的主動箝位返馳式轉換器,其特點是將存於變壓器的漏電感能量進行回收,同時功率開關可達成零電壓切換(zero voltage switching;ZVS)。但當系統的等效集總電容較大時,需要足夠的漏電感才能使功率開關達成零電壓切換,不但提升變壓器的設計難度,可能甚至需額外增加電感器。綜上所述,若能確切掌握系統的等效集總電容之組成,有助於提升轉換器效能的設計。
為了讓設計者在設計階段就可準確掌握系統的等效集總電容,本文將介紹變壓器模型與其阻抗特性、量測變壓器模之阻抗及半導體元件的寄生電容、實際分析並推導返馳式轉換器的等效集總電容,最後實測樣機將選用立錡PWM控制IC RT7736返馳式轉換器作為範例說明,以電路模擬與實測結果驗證理論的推導。
變壓器模型與其阻抗特性
返馳式轉換器中所用的變壓器並非理想的變壓器,如前所述,在快速切換時,其變壓器的漏電感會與系統的等效集總電容產生高頻振鈴及高壓突尖。如圖3所示,變壓器的分佈電容其實也是系統的等效集總電容之構成元素之一;若能充分掌握變壓器的特性,特別是阻抗特性曲線,就更能掌握系統的性能。本文所分析的變壓器特性是採用Bruno Cogitore所提出的雙繞組變壓器(two-winding transformer)的一等效模型,如圖4所示,詳情可參考文獻[1]。圖5則為典型雙繞組變壓器之阻抗特性曲線的漸近示意圖,圖中紅色實線為次級側開路時的初級側阻抗(ZOC)曲線,藍色實線為次級側短路時的初級側阻抗(ZSC)曲線。
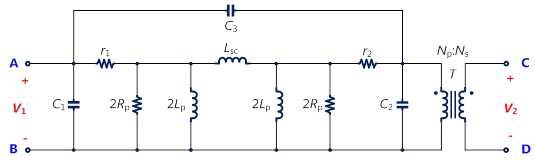
圖4 雙繞組變壓器之一等效模型示意圖
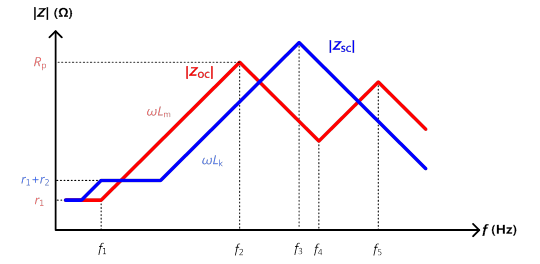
圖5 典型的雙繞組變壓器阻抗特性曲線之漸近示意圖
由圖5的阻抗特性曲線可得圖4中變壓器的相關參數,相關的關係式如下:
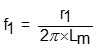 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
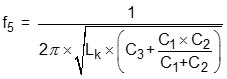 (5)
(5)
其中,Lm和LK雖未出現在圖4之電路模型中,其與模型元件之關係可見式(6)至(7)。Lm為變壓器初級側的開路電感,也就是變壓器之激磁電感(magnetizing inductance);Lk為變壓器初級側的短路電感,也就是變壓器之漏電感(leakage inductance;Lk)。參考圖5,由紅色的阻抗特性曲線之第一上升斜率與f1,f2,f4,f5,可得變壓器之開路電感Lm、初級側的繞線電阻r1、及分佈電容C1+C2;而由藍色的阻抗特性曲線中之第一上升斜率與f3,可得變壓器次級側映射至初級側的繞線電阻r2之和r1+r2、短路電感LK及分佈電容C1+C3。圖4的三個分佈電容C1、C2及C3之值可由式(2)至(4)計算出來,因屬曲線擬合(curve fitting)之等效電路模型,計算出之個別電容值有可能為負值。
 (6)
(6)
 (7)
(7)
藉由量測變壓器初級側開路時的次級側阻抗(Z'OC)曲線,可得次級側之激磁電感,故變壓器之匝數比可表示如下:
 (8)
(8)
其中,Lm為變壓器初級側之激磁電感,L’m為變壓器次級側之激磁電感。
在圖4中,RP代表鐵芯損失,r1代表一次測的繞線電阻,r2代表二次測映射至初級側的繞線電阻。若滿足等式(9)的條件,則RP、(r1+r2)及r1和r2可被忽略;因變壓器中的分佈電容C3在較高頻才有影響,在本文的分析中亦先忽略不計,所以變壓器的分佈電容CD_T可表示如式(10)。變壓器的模型因此可簡化如圖6所示之電路圖。下一章「返馳式轉換器的等效集總電容分析」將採用此簡化之變壓器模型。
RP » ωLm (9a)
r1 + r2 » ωLk (9b)
CD_T = C1 + C2 (10)

圖6變壓器之簡化雙埠模型示意圖
返馳式轉換器的等效集總電容分析
如上所述,為了降低功率開關和輸出二極體所受的電壓應力(voltage stress)及防止高電壓突尖損壞半導體元件,通常會分別在初級側和次級側加上一電壓箝位電路(voltage clamp circuit)及一緩振電路,如圖7所示。因此,為能完整考量到所有寄生元件,本文在分析返馳式轉換器的等效集總電容時,也將此二實際應用電路併入分析。圖7中的元件符號分別定義DVC為電壓箝位電路的二極體,Cj_Dvc為電壓箝位電路的二極體接面電容,CVC為電壓箝位電路的電容,CSN為緩振電路的電容,RCB為輸入電容的等效串聯電阻(ESR),RCo為輸出電容的等效串聯電阻,RVC1以及RVC2為電壓箝位電路的電阻,RSN為緩振電路的電阻。

圖7 含初級側電壓箝位電路與次級側緩振電路的返馳式轉換器電路圖
以下將分別探討初級側與次級側的等效集總電容:
˙ 簡化次級側的緩振電路
圖8為返馳式轉換器的次級側電路圖,含緩振電路及寄生元件,其中,CSN為緩振電路的電容,RSN為緩振電路的電阻。
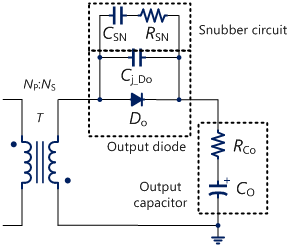
圖8 返馳式轉換器的次級側含寄生元件之電路圖
Cpri_eq代表轉換器次級側之合併電容Csec_eq映射至初級側之電容,其關係式為
 (11)
(11)
其中, , (12)
, (12)
Xsec_eq為Csec_eq之電容抗,如式(13),
 (13)Zsec_eq代表次級側之阻抗,其虛數部分即為次級側合併之電容抗Xsec_eq,且XSN為CSN之電容抗、Xj_Do為Cj_Do之電容抗、Xo為Co之電容抗及ZSN為緩振電路之阻抗,由電路可得以下之關係式:
(13)Zsec_eq代表次級側之阻抗,其虛數部分即為次級側合併之電容抗Xsec_eq,且XSN為CSN之電容抗、Xj_Do為Cj_Do之電容抗、Xo為Co之電容抗及ZSN為緩振電路之阻抗,由電路可得以下之關係式:
 (14)
(14)
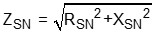 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
上述式中之頻率fr為系統操作在非連續導通模式(discontinuous conduction mode;DCM)時,在功率開關上之電壓因變壓器之激磁電感與系統的等效集總電容所引發之振鈴的頻率,如圖2所示,此頻率fr一般約為數百kHz。本文之分析中會實際量測此頻率,所以相關阻抗之化簡,均以此頻率時之電容抗值作比較。若緩振電路中所用的電容值CSN較小時,在頻率fr下,電容抗XSN遠大於電阻RSN,所以RSN電阻可被忽略,則緩振電路的阻抗ZSN僅有電容抗XSN。同理類推,所使用的輸出電容值CO通常遠大於輸出二極體的接面電容(Cj_Do)與緩振電路電容(CSN)相加之和,因此輸出電容也可被忽略。綜合上述,可得次級側之合併電容Csec_eq,並可將式(11)簡化為
 (19)
(19)
˙ 簡化初級側的電壓箝位電路
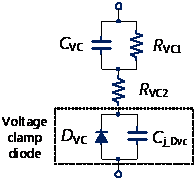
圖9 返馳式轉換器的初級側含寄生元件之電壓箝位電路圖
初級側的電壓箝位電路主要由電阻、電容以及二極體所組成,如圖9所示。從圖中可推導出其等效電容為
 (20)
(20)
其中,
 (21)
(21)
 (22)
(22)
 (23)
(23)
圖9的電容CVC與RVC1為並聯形式,若採用較大電容CVC時,則電容抗-jXVC會較小,並遠小於電阻值RVC1,則電阻可忽略不計,式(21)可因此化簡為
 (24)
(24)
再者,電壓箝位電路的二極體反向電壓與輸入電壓呈正比,且二極體的反向電壓與其接面電容呈反比,所以在全範圍(universal input, 90Vac~265Vac)的輸入電壓情形下,根據廠商所提供規格書的接面電容特性曲線圖,其接面電容約為數皮法拉(pF, 1p=10-12),若二極體的接面電容的容抗值-jXj_Dvc遠大於電壓箝位電路的電阻RVC2,則RVC2也可忽略,因此可將等式(24)改寫為
 (25)
(25)
最後,電壓箝位電路的電容與二極體的接面電容形成串聯,根據上述的假設條件下,若二極體的接面電容抗遠大於電壓箝位電路的電容抗,也就是二極體的接面電容值遠小於電壓箝位電路的電容值CVC,則電壓箝位電路的電容也可被省略,因此電壓箝位電路的等效集總電容主要由二極體的接面電容主宰。
 (26)
(26)
˙ 返馳式轉換器的等效集總電容
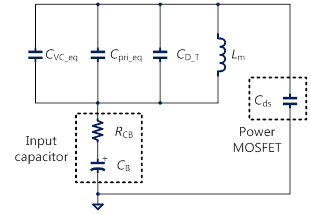
圖10 返馳式轉換器的等效集總電容電路圖
經由上述的分析過程後,可將返馳式轉換器的等效集總電容整理成圖10所示。在實務應用上,為避免輸入電容上的電壓漣波過低,致使半導體元件的電流應力較大,一般會使用較大的輸入電容,造成輸入電容的阻抗(ZCB)遠小於變壓器分佈電容的阻抗(ZD_T)、電壓箝位電路的阻抗(ZVC_eq)、及變壓器次級側電路映射至初級側的阻抗(Zpri_eq)之等效並聯阻抗,故可忽略輸入電容的影響,所以系統的等效集總電容等式可簡化為
 (27)
(27)
綜合上述,可得前述之振鈴頻率如下式:
 (28)
(28)
故本文將在電路模擬與實例上,量測因變壓器之激磁電感與系統的等效集總電容所引發之振鈴的頻率fr,用以推算系統的等效集總電容。
元件特性之量測
經由上述的分析,已對系統的等效集總電容有充分的瞭解。半導體元件的電容特性雖然有廠商提供的規格書可參考,然而規格書中常未能提供交流電源全範圍輸入電壓條件下的數據。本章將介紹如何量測變壓器及半導體元件的特性,並從實例中作說明。圖11為RT7736返馳式轉換器的電路圖,其轉換器的基本規格以及元件參數如下:
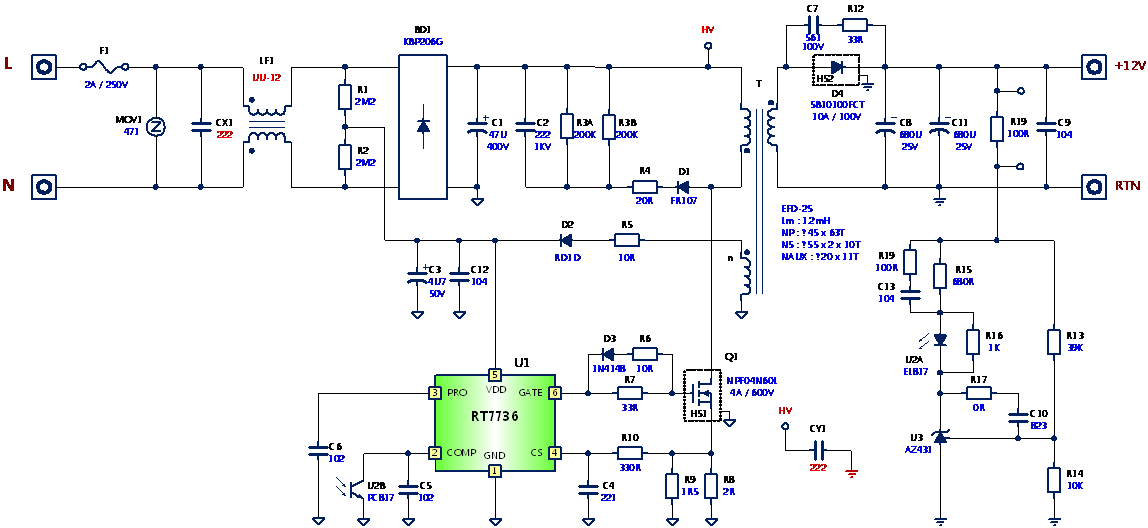
圖11 RT7736返馳式轉換器電路圖
輸入電壓VIN:90Vac-265Vac;
輸出電壓VO:12V;
負載電流IO:2A;
變壓器T:EFD-25;
激磁電感Lm:1.2mH;
匝數比n:6.3 (63:10)
輸入電容CB:47μF/400V,等效串聯電阻RCB:0.68Ω
輸出電容CO:1.36mF/25V,等效串聯電阻RCo:20mΩ
功率開關Q:NPF04N60L,600V/4A;
輸出二極體DO:SB10100FCT,100V/10A;
電壓箝位電路的二極體DVC:FR107,700V/1A;
電壓箝位電路的電容CVC:2.2nF/1000V;
電壓箝位電路的電阻RVC1、RVC2:200kΩ、200kΩ;
緩振電路的電容CSN:560pF/100V;
緩振電路的電阻RSN:33Ω。
I. 變壓器的阻抗特性測量
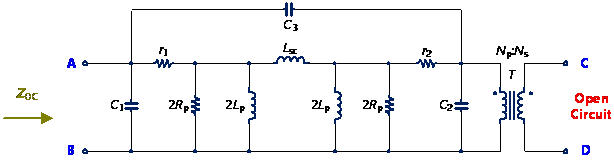
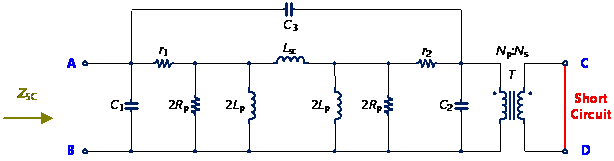
磁性元件的特性雖困擾著電源工程師,如鐵芯材質的差異,造成磁飽和、鐵芯損失以及繞線的電阻特性(如集膚效應與鄰近效應)等,但理論上這些元件資訊可由阻抗對頻率的特性曲線上獲得。然而,大多數的磁性元件製造商卻沒有提供這樣的資訊,因此本節將介紹如何量測變壓器阻抗對頻率的特性以及從阻抗曲線中設法取得模型的電路元件參數。最常見變壓器的阻抗特性是在次級側分別為開路和短路的條件下測量初級側的阻抗,其量測方式如圖12所示[2]。
本文中是使用Wayne Kerr Electronics 6500B精密阻抗分析儀(Precision Impedance Analyzer)量測所選用的EFD-25變壓器之阻抗特性,圖13即為所量測到的變壓器阻抗曲線。變壓器的模型是複雜的,因為模型中所有電阻和電感是非線性的,繞線電阻隨頻率增加而增加,鐵芯損失則是與頻率、溫度和激磁電流有關係。
(a)
(b)
圖12 變壓器的阻抗特性量測示意圖 (a)次級側開路,(b)次級側短路
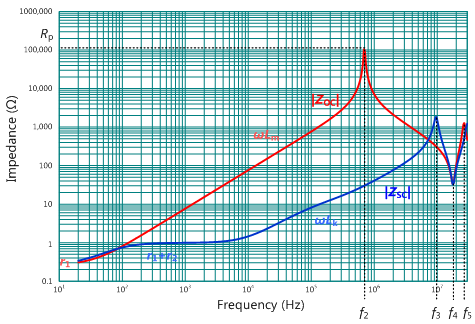
圖13 EFD-25變壓器的阻抗特性曲線圖
在實務應用上,因系統效率、變壓器溫升以及EMI的問題,使變壓器的繞線結構呈多元化,而其特性亦會隨之改變,但此變化不在本文討論範圍內。如前所述,從圖13的變壓器特性曲線中可得知變壓器的激磁電感值、漏電感值、鐵損電阻、初級側與次級側的繞線電阻以及各個諧振頻率點,將所得之變壓器特性參數列於表1。將此變壓器特性參數,代入式(2)至(4),即可計算出變壓器的分佈電容值,亦如表1所示。
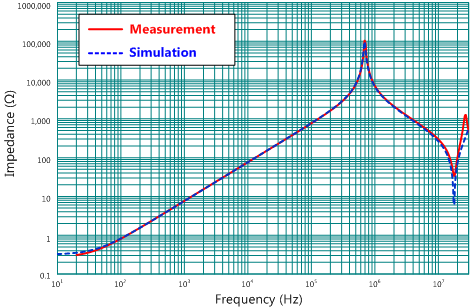
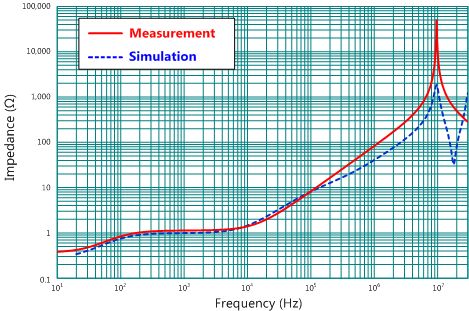
本文為了方便計算與分析,藉由SIMPLIS電路模擬軟體來比較與量測結果的差異,圖14為變壓器的SIMPLIS模擬電路圖,圖15為變壓器阻抗的模擬與量測比較圖,圖中的紅色實線為量測的結果,藍色虛線為SIMPLIS電路模擬的結果。從圖中可看出在低頻段範圍有較好的吻合度,但在高頻段部分因模型的階次較低,誤差較大,然而在實務應用上,高頻段的部分影響不大。
表1 EFD-25變壓器的特性參數
|
初級側激磁電感Lm(H)
|
1.2m
|
頻率f2(Hz)
|
686k
|
|
次級側激磁電感L’m(H)
|
32.2μ
|
頻率f3(Hz)
|
9.6M
|
|
漏電感Lk(H)
|
13.2μ
|
頻率f4(Hz)
|
17.6M
|
|
鐵損電阻Rp(Ω)
|
104k
|
頻率f5(Hz)
|
27M
|
|
初級側繞線阻抗r1(Ω)
|
269m
|
變壓器的分佈電容C1(F)
|
29.5p
|
|
次級側繞線阻抗r2(Ω)
|
769m
|
變壓器的分佈電容C2(F)
|
14.8p
|
|
|
|
變壓器的分佈電容C3(F)
|
-8.6p
|
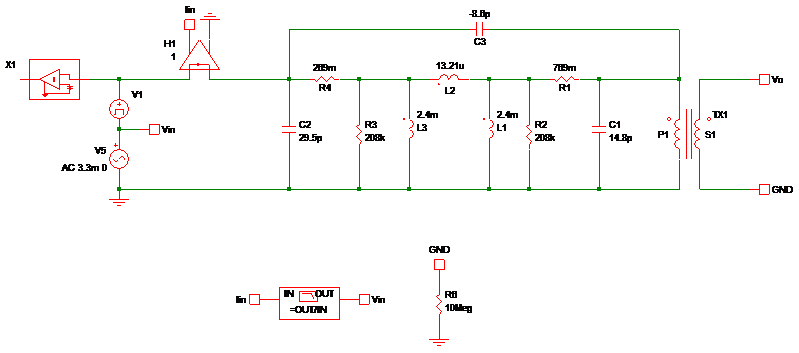
圖14 變壓器的SIMPLIS模擬電路圖
(a)
(b)
圖15 EFD-25變壓器阻抗特性的模擬與量測比較圖(a)次級側開路,(b)次級側短路
II. 量測功率開關與二極體的電容特性
功率開關及二極體的寄生電容特性曲線可從規格書或由LCR電錶測量獲得。圖16(a)為典型功率開關的寄生電容電路圖,主要由為閘-汲極電容(gate-drain capacitance;Cgd)、閘-源極電容(gate-source capacitance;Cgs)、汲-源極電容(drain-source capacitance;Cds)所組成;圖16(b)為典型二極體的寄生電容電路圖,主要有一接面電容(junction capacitance;Cj)。而一般在功率開關的規格書中主要描述輸入電容(input capacitance;Ciss)、輸出電容(output capacitance;Coss)以及反向轉移電容(reverse transfer capacitance;Crss),其組成電容如下列關係式:
 (29)
(29)
 (30)
(30)
 (31)
(31)
如式(27)所示,與系統的等效集總電容有關的是功率開關的輸出電容及二極體的接面電容。然而,規格書常僅提供數十伏特的輸出電容特性曲線,所以無法滿足全範圍的輸入電壓。
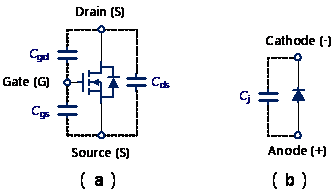
圖16 (a)功率開關及(b)二極體的寄生電容電路圖
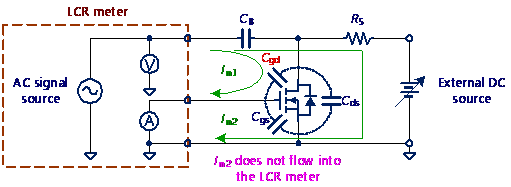
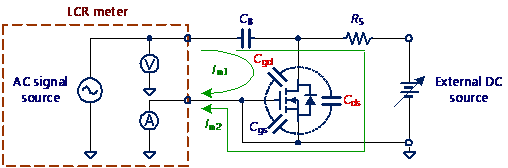
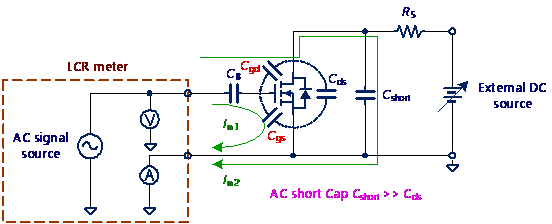
本文使用Keysight Technologies E4980A 精密型LCR錶(Precision LCR Meter)。而因一般LCR錶內建的最大直流電壓限制為40V,也需額外的高壓直流電源供應器進行量測,因此另搭配Keithley 2410 SourceMeter。其量測示意圖可參考圖17與18所示及參考文獻[3]。
(a)
(b)
(c)
圖17 功率開關的寄生電容特性量測示意圖 (a)Crss,(b)Coss,(c)Ciss
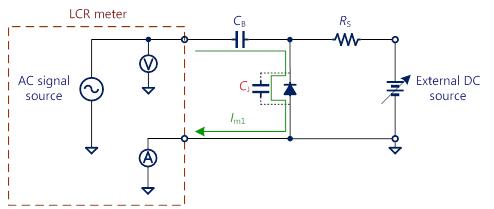
圖18 二極體的接面電容量測示意圖
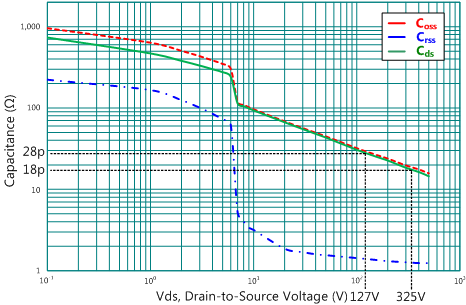
選用的功率開關為NPF04N60L,輸出二極體為SB10100FCT,電壓箝位電路的二極體為RF107,其電容特性曲線如圖19所示,從圖中可看出電容值均和電壓有關,電壓愈高,寄生電容愈小,且當功率開關的汲-源極電壓越高時,則輸出電容越小,且將使輸出電容(Coss)幾乎為汲-源極電容(Cds),所以在全範圍的輸入電壓時,亦可用汲-源極電容進行探討。
(a)

(b)
圖19 寄生電容的特性曲線圖 (a)功率開關,(b)二極體
範例
I. 理論計算
本文是以立錡科技PWM控制IC RT7736的返馳式轉換器為實測平台,其電路圖與參數如圖11及表2所示,且工作條件分別為輸入電壓90Vac及230Vac,輸出電壓均為12V,輸出電流100mA,並使轉換器操作在不連續導通模式。先探討輸入電壓為90Vac:
(a) 功率開關的汲-源極電容(Cds)、輸出二極體的接面電容(Cj_Do)以及電壓箝位電路的二極體(Cj_Dvc)以及相關參數可由圖11及19而得知,並將其數值及外加電路元件之參數列於表2。
表2 RT7736返馳式轉換器的元件參數
|
功率開關的汲-源極電容Cds
|
28pF@127Vin
18pF@325Vin
|
緩振電路電阻RSN
|
33Ω
|
|
輸出二極體的接面電容Cj_Do
|
115pF@127Vin
80pF@325Vin
|
緩振電路電容CSN
|
583pF
|
|
輸入電容CB
|
47μF
|
電壓箝位電路電阻RVC1
|
100kΩ
|
|
輸入電容ESR RCB
|
0.68Ω
|
電壓箝位電路電阻RVC2
|
20Ω
|
|
輸出電容Co
|
1.36mF
|
電壓箝位電路二極體的接面電容Cj_Dvc
|
3.7pF
|
|
輸出電容ESR RCo
|
20mΩ
|
電壓箝位電路電容CVC
|
2.2nF
|
(b) 變壓器的分佈電容可由圖13的變壓器阻抗特性曲線得知諧振頻率點,用等式(2)至(4)計算分佈電容(C1、C2及C3),最後可由等式(10)計算出。
 (32)
(32)
(c) 計算次級側緩振電路的等效集總電容前,需設定fr頻率以估算緩振電路的阻抗,根據實務經驗fr約為500kHz,則由等式(11)、(13)與(14)可計算出等效集總電容計算如下,
 (33)
(33)
 (34)
(34)
 (35)
(35)
由等式(33)中可看出緩振電路的阻抗幾乎等於電容抗,
 ( 36)
( 36)
所以亦印證可將此電阻省略。再由等式(33)中可觀察出輸出電容的電容抗遠小於輸出二極體的接面電容與緩振電路之電容抗總和,所以輸出電容可忽略不計,因此亦印證由等式(19)也可獲得相同的結果。
 (37)
(37)
(d) 同理,由等式(20)與(21)可計算出電壓箝位電路的等效集總電容為
 (38)
(38)
 (39)
(39)
由上式可看出電壓箝位電路的等效集總電容由二極體的接面電容主宰,所以也可忽略電壓箝位電路的電阻與電容的影響,如等式(26)。
 (40)
(40)
(e) 最後由等式(27)可計算出輸入電壓為90Vac時返馳式轉換器的等效集總電容為:
 (41)
(41)
同理類推,輸入電壓為230Vac,功率開關的汲-源極電容變更為18pF,輸出二極體的接面電容亦改為80pF,再重複上述(a)至(e)的計算過程亦可得返馳式轉換器的等效集總電容為82.7pF。
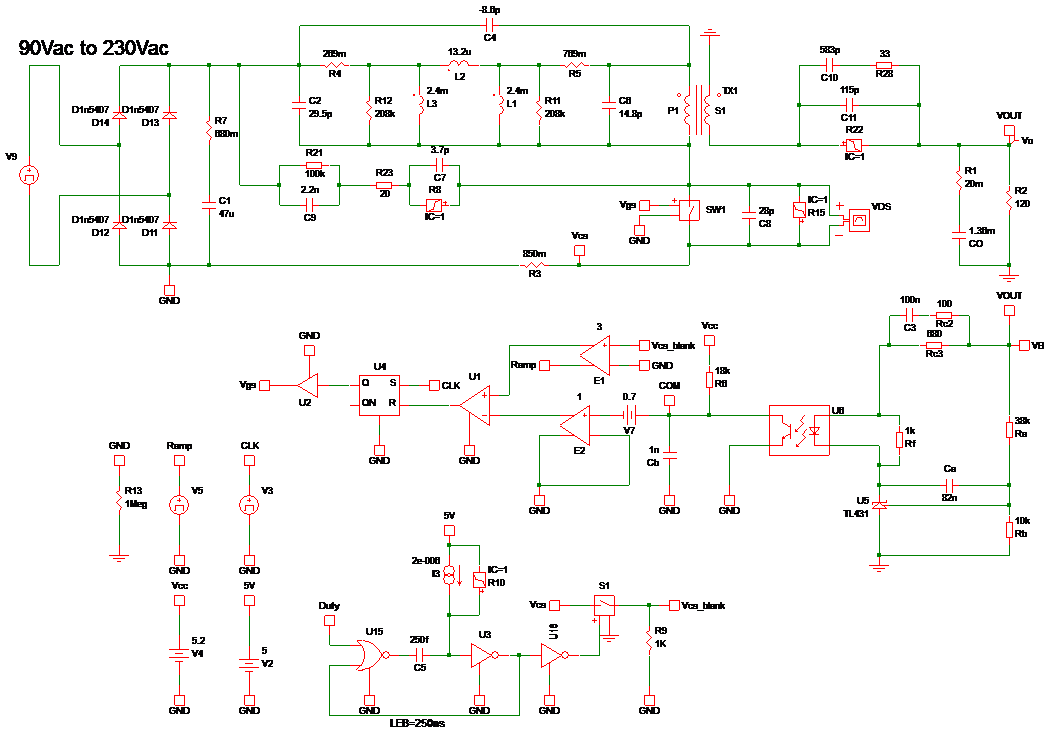
圖21 返馳式轉換器的SIMPLIS模擬電路圖
II. 電路模擬與測量
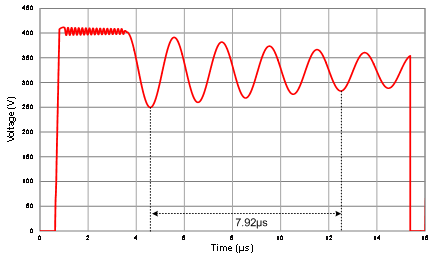
本文將利用SIMPLIS電路模擬軟體和實例量測的結果進行驗證。圖21為返馳式轉換器的SIMPLIS電路模擬圖,圖22與23為利用SIMPLIS電路模擬與實例的功率開關的汲-源極的電壓波形圖,表3為理論計算、SIMPLIS電路模擬與實例的結果比較表。根據結果可看出理論計算、電路模擬與實測具有良好的一致性。

(a) (b)
圖22 模擬功率開關的汲-源極端的電壓波形圖 (a)90VAC,(b)230VAC
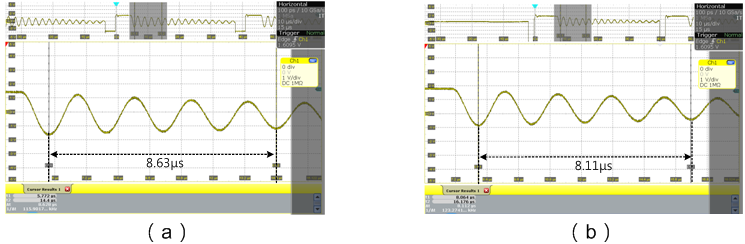
圖23 測量功率開關的汲-源極端的電壓波形圖 (a)90VAC,(b)230VAC
表3 系統的等效集總電容比較表
|
輸入電壓
|
90Vac/60Hz
|
230Vac/50Hz
|
|
頻率
fr
|
等效集總電容
Csys
|
頻率
fr
|
等效集總電容
Csys
|
|
理論計算
|
474.9kHz
|
93.6pF
|
505.2kHz
|
82.7pF
|
|
電路模擬
|
473.9kHz
|
94.0pF
|
505.1kHz
|
82.8pF
|
|
實例測量
|
463.6kHz
|
97.0pF
|
493.2kHz
|
85.7pF
|
|
|
|
|
(a) |
(b) |
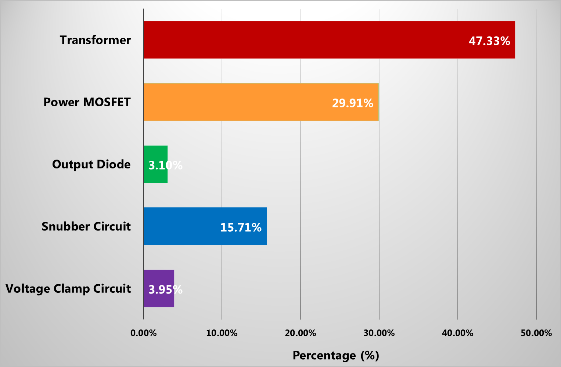
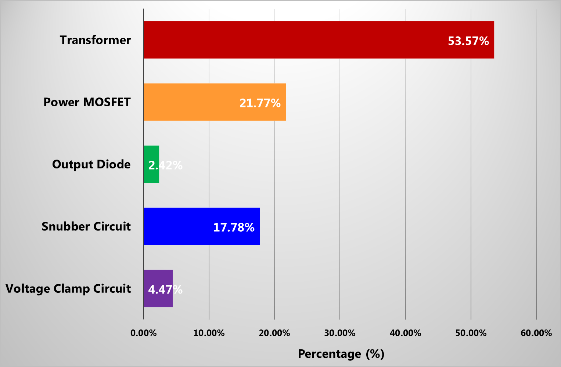
圖24 各元件占電路的等效集總電容之百分比 (a)90VAC,(b)230VAC
如前所述,許多文獻皆顯示等效集總電容為功率開關的輸出電容,但透過本文理論的分析可知變壓器、輸出二極體、緩振電路以及電壓箝位電路均有所貢獻,且從圖24中又可觀察得知各元件所占等效集總電容的比例以變壓器的分佈電容為最高,功率開關的汲-源極電容次之,再其次是緩振電路的電容。若以此為例,要有效地降低系統的等效集總電容,則改善變壓器繞線方式或結構以減少分佈電容是為較佳的方式。
結論
返馳式轉換器的等效集總電容主要為變壓器、半導體元件以及緩振電路所構成的,故變壓器的阻抗特性與測量半導體元件的寄生電容特性是本文分析與探討的重點。本文詳細介紹了變壓器的阻抗特性與量測方法、半導體元件的寄生電容量測,並且用理論推導方式分析返馳式轉換器的等效集總電容,同時說明了各元件對系統的等效集總電容的貢獻度,以提供給設計者作為設計參考。
參考文獻
1. Bruno Cogitore, Jean Pierre Kéradec, and Jean Barbaroux,”The two-winding transformer: an experimental method to obtain a wide frequency range equivalent circuit,” IEEE transactions on instrumentation and measurement, vol. 43, pp.364-371, April 1994.
2. Ray Ridley, “Transformer Impedance Measurements,” Ridley engineering.
3. Hisao Kakitani and Ryo Takeda, “Increasing importance of capacitance measurement,” Agilent Technologies international, Japan Ltd.