摘要
本篇應用指南將介紹由效率觀點,對應定頻操作flyback 轉換器,設計合適的感量,變壓器,和圈比。如何用數學模型推導有可能的最佳效率設計,最後在以實務上的元件損耗量測方式,驗證理論數據。
1. 前言
返馳轉換器(flyback converter)是應用最廣泛的電源拓樸之一。 由於返馳轉換器的零件數最少,成本低,也是被廣泛應用的原因之一。
Flyback 轉換器已被廣泛的用在100W以下的離線電源,包括印表機、筆記型電腦、顯示器、家電設備以及諸多電子電氣產品。圖一為Flyback 轉換器的功率電路圖。

圖一、Flyback 轉換器電路圖控制IC透過閘極腳位驅動返馳式
輸入電壓Vin 來自市電輸入,經橋式整流與大電容濾波,一般而言,其範圍約在90Vdc 至370Vdc。Flyback轉換器主要涵蓋了一個開關晶體(Q),一個續流二極體(D),一組變壓器(T)以及一個輸出電容(Co)。在一般應用峰值電流控制(peak
current mode control)的架構裡,電阻RCS用來檢知初級側電流(iLP)波型。這裡說的變壓器,其實是耦合電感器,包含初/次級線圈(匝數分別為
NP與NS),以及對應的電感值 (LP與LS)。 只要給定一組操作點,即輸入電壓與負載電流,Flyback轉換器就會運行在一個穩態的模式。所謂穩態模式是指一組固定的電壓與電流波型。穩態模式又可分為兩類,其一為連續電流導通模式(Continuous
Conduction Mode, C.C.M.) 另一為非連續電流導通模式(Discontinuous Conduction Mode, D.C.M.)。
【設計重點與觀念】
本設計概要就是探討如何來決定三個關鍵參數。從運行模式(C.C.M/D.C.M)方程式知,以下幾個參數決定了整個轉換器的運行。
1. 工作頻率 (fS)
2. 初(次)級電感量 (LP或LS)
3. 變壓器匝數比 ( )
)
這三個關鍵參數不僅影響了Flyback轉換器的運行特性模式,同時也決定了轉換器的效率、成本與體積。這是因為同時也決定了開關晶體與二極體的電壓電流應力以及輸出電容的漣波電流。當然對於變壓器的繞線與整個體積也直接相關。
1. 開關頻率(Switching Frequency)
眾所周知,開關頻率越高,可以減小整個轉換器的體積。但是隨之而來的是轉換效率的降低以及EMI問題的難解。一般而言,在一個離線的Flyback 轉換電路中,開關頻率多半在幾十kHz。現行市售的轉換器控制IC多半將開關頻率設定在IC內部,多為65kHz左右。這樣的頻率等同於在效率、體積與
EMI問題,選擇一個折衷點。
2. 變壓器的匝數比(n)
假設轉換器在C.C.M運行模式下,

n為匝數比
當匝數比決定了,也就意味著隨著輸入電壓的改變,工作週期(duty cycle, D)也跟著變化。在最低輸入電壓Vin,min與最大負載IO,max下,責任週期將出現最大值,Dmax。

如果將 定義為Vro,可以聯想與開關晶體與二極體的電壓應力直接相關,以下將以此參數為變數,在設計上會更為直觀。
定義為Vro,可以聯想與開關晶體與二極體的電壓應力直接相關,以下將以此參數為變數,在設計上會更為直觀。

換句話說,決定了最大工作週期或者Vro就決定了變壓器匝數比,同時也決定了與開關晶 體與二極體的電壓應力。雖然說,與開關晶體與二極體的電壓應力還必須考慮到變壓器漏電感造成的電壓突尖(voltage
spike)與緩衝電路(snubber)的設計,不過以設計裕量的觀點來看,(4)與(5)也是選擇功率器件的主要參考。
如果換句話說,Vro或者n圈數比的設計,事實上是一二次側電流,在一切換週期內的比例分配,不論轉換器勢操作在C.C.M或者D.C.M的狀態下。如果Vro小,相對應的二次側的電流峰值和均方根值都會較小,一次側則會變大,(在相同的一次側感量條件下),如果Vro大,則結果相反。以下則會探討利用Vro當變數,對整體效率的影響。
在峰值電流模式控制的轉換器中,工作週期大於0.5 時,會有次諧波振盪(sub-harmonic oscillation)的問題,必須在迴路中有外加斜坡(external
ramp)。在新型Flyback 控制器中,通常已經內置斜率補償了,所以不必擔心有次諧波振盪的問題。
3. 初(次)級電感量(LP, LS)
當匝數比確定以後,

電感量的大小對應的是電流斜率的高低。圖二為次級側電流的波形。

圖二、次級側電流波形
其中斜坡部分,

利用梯形面積可求得輸出電流IO,

當iLSK = iLS時,就是C.C.M 與D.C.M 的邊界電流,IOB,也就是

在此定義一個漣波因數(ripple factor, Krf)為

也就是斜坡大小除以梯形兩邊高度和。將(10)代入可得從(10)式可以看出Krf代表著有多少比例的負載電流工作在C.C.M,多少比率的電流工作在D.C.M。舉例來說,表示有60%的電流工作在C.C.M,40%工作在D.C.M。
從(8)式可以看出電感LS大時, lOB也變高,Krf也變高。也就是說,Krf與LS有直接的關係。Krf將被用來定義電感大小的重要參數。
從”返馳轉換器工作原理”中,轉換器運行存在一條C.C.M/D.C.M 邊界曲線:

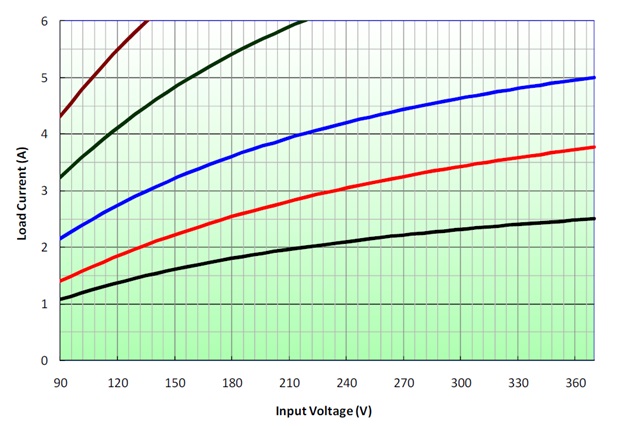
圖三、對應不同電感值的C.C.M/D.C.M 邊界曲線
圖三為對應不同電感值的C.C.M/D.C.M邊界曲線。曲線的下方表示D.C.M區域,曲線上方表示C.C.M區域。
黑色曲線代表最大的電感,同時大部分的工作點將落在C.C.M(假設滿載電流為5A)。棕色曲線表示電感值最 小,幾乎所有工作點都落在D.C.M 區域。一旦電感值確定,就存在唯一的一條C.C.M/D.C.M
邊界曲線了。以藍色曲線為例,(90V, 2.2A)與(240V, 4.2A)代表同一的電感值的轉換器。
依照以上的說明,設計工程師只要定義了在最低輸入電壓下的Krf值,就等同定義了電感值了,這樣的理解,有助於電感大小的取決。
到底Krf選擇多大最為適當呢?以下本篇指南,會以Krf為第二個變數,在選定的變壓器下,推導出可能效率最佳化的Krf值。請注意,這樣的設計出發點,只考慮滿載輸出的效率狀況,間接反映在滿載狀況的溫昇,但現實上,由於現行的能效法規定義效率是25%,50%,75%和
100%四點的平均效率,所以在實務上,並不見得滿載狀況,是效率最佳點,只要散熱能在安全規範下。但由於控制器在輕載控制策略的多元化,有可能是降頻操作或者是cycle
skip mode,使得數學模型更為複雜,則不在本文的討論範圍內。
從變壓器體積與轉換效率的觀點出發,一般的經驗法則,加上許多實務量測結果,離線Flyback轉換器在最低輸入電壓時的Krf的最佳值約為0.4。對到圖三的藍色曲線,如果是單一高壓輸入(220Vac)系統,就取在0.8左右最為適當。
【電壓電流計算】
一旦變壓器參數確立了,不同工作點運行時的器件電壓與電流就可以透過工作原理輕易計算出來。
C.C.M
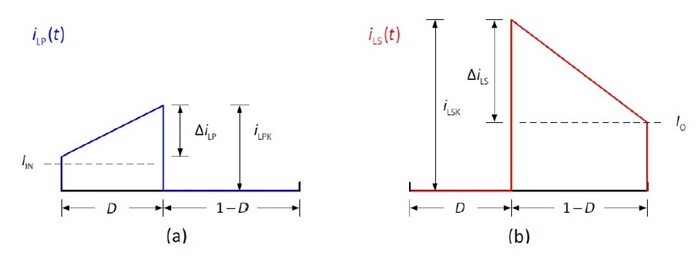
圖四、為C.C.M 初次級側電流波形圖
以下是基於最低輸入電壓下,定義Vro與漣波因數Krf下,計算電感值與各電流參數的公式與順序:
(1) 利用定義好的Vro,得出最大工作週期Dmax,計算出變壓器初次級匝數比

對應方程式(4)、(5)如第二頁,事實上Vro已可以選定所需的MOSFET和Diode耐壓。
(2) 以Krf和Vro為變數,設計所需的感量。

(3) 以設計出的感量,後續的電流波形,峰值、均方根值都可以依續推導。

Input current:

流經輸出電容的等效電流

流經輸入電容的等效電流高頻電流

實務上,離線flyback 轉換器,流經輸入電容的交流電流還包含交流輸入電流的漣波120Hz,但這部分的電流除了效率差異外,不會與Krf、Vro相關。
因為(17)~(23)式是基於最低輸入電壓與最大負載電流計算出來的,所以
- 開關晶體的最大電流應力

- 初級繞組的最大RMS 電流

- 次級二極體的最大平均電流

- 次級繞組的最大RMS 電流

- 輸出電容的最大RMS 電流

- 輸入電容的最大RMS 電流

這些數值關係到功率半導體的選用以及變壓器鐵芯選擇(繞線粗細有關)。
D.C.M
由於D.C.M 操作模式,Krf = 1,輸入輸出電流各有其他的公式,本文不另行推導,詳細請見”定頻返馳式轉換器設計指南”。
2. 元件損耗的估算
本章節將以Krf、Vro為變數,帶出功率元件的一些損耗公式,藉由數學模型,我們有機會可以在設計理論上推導出最佳工作點。
(1) Bulk CAP loss:

(2) MOSFET conduction loss:

(3) MOSFET switching loss:

上述的切換損失,用簡化的方式計算on/off loss,這裡假設on/off交越時間都為Tcross,切換時的電流都用 近似。
近似。
(4) Current sense loss:

(5) Snubber loss:
假設變壓器的漏感為 ,定義VZ為MOSFET
clamping電壓,clamping電路為ZCD架構,(雖然一般應用為RCD架構,能節省材料成本,但為簡化數學模型,用VZ取代,損耗在滿載是可以近似的)。假設
,定義VZ為MOSFET
clamping電壓,clamping電路為ZCD架構,(雖然一般應用為RCD架構,能節省材料成本,但為簡化數學模型,用VZ取代,損耗在滿載是可以近似的)。假設

(6) Diode loss:
輸出整流器的損耗是為Id(t)·VF(Id(t))的積分,為了簡化數學模型,可用固定的VF和RD代表。
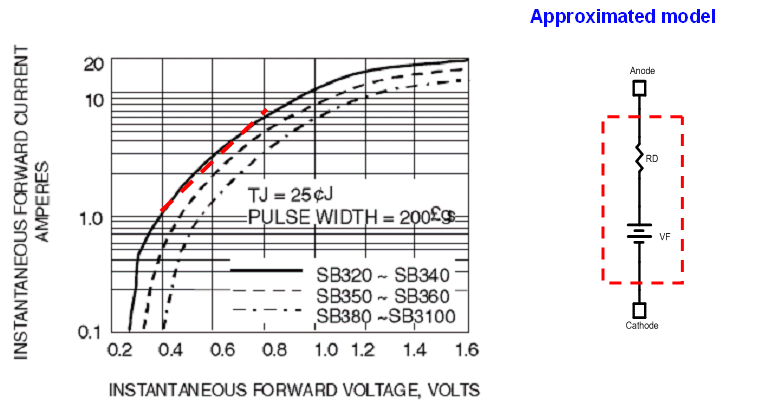
圖五、輸出整流器等效模型
簡化後的數學模型,Id(t)·(VF + RD·Id(t))的積分,可等效為:

由於ID vs VF,並非線性的曲線,而是指數曲線,所以等效RD並非定值,而會隨 工作點改變,事實上ID電流越大,或者轉換器在較深的C.C.M,等效RD變小,整流器的損耗可以直接用
工作點改變,事實上ID電流越大,或者轉換器在較深的C.C.M,等效RD變小,整流器的損耗可以直接用
 近似。
近似。
(7) Output CAP loss:
輸出電容損耗則為:

(8) Transformer copper loss:
變壓器損耗的估算則是更為複雜的數學模型,首先鐵心的選擇可用面積乘積法設計,詳細的變壓器設計請參考”返馳變壓器設計指南”。
首先,變壓器鐵芯的選擇,必須要讓足夠線號的銅線繞得進去,同時鐵芯又不能飽和。這裡就牽涉到三個重要的參數,最大磁通密度(Bmax)、最大電流密度
(Jmax)以及最大繞線因數(kmax)。
(a) 最大磁通密度 (Bmax)
性鐵芯都會飽和,飽和磁通密度(Bsat)指在某個磁場強度(H)下,磁通密度不再隨H改變而變的磁通密度。以功率鐵氧體(ferrite)而言,在 25°C下,飽和磁通密度達5,100高斯(Gauss),或是0.51特斯拉(Tesla);在100°C下,飽和磁通密度約為3,900高斯。以一般峰值電流控制法的Flyback變壓器,最高的工作磁通密度可定在3,000高斯左右,避免高溫下鐵芯飽和。
(b) 最大電流密度 (Jmax)
電流密度的定義為單位導線面積所通過的電流量。在設計上通常需要規範一個所謂安全電流密度,避免因電流密度高造成銅損太大而溫昇過高,影響可靠度與安全。一般依週溫與冷卻的條件而定,有些以J
= 250 ~ 650 A/cm2為準則,有人習慣用 1/J = 350 ~ 750cmil/A。兩者大致上所代表的意義差不多。(1cm2
= 197,350 cmil)。電流密度的高低影響銅損的大小,而銅損則為損失總合的一大部份。所以在可能的範圍下,應提高繞線因數,降低電流密度,這對改善耦合電感的溫昇有絕對的幫助。
(c) 最大繞線因數 (kw,max)
所有鐵芯都有一定的繞線窗(winding window),實際導線所佔面積與繞線窗面積(window area,Wa) 之比稱為繞線因數。繞線因數受到幾個因素的影響,分別為漆包線的絕緣厚度、漆包線排列所餘空間、法拉第屏蔽及其他絕緣物(如繞線架(bobbin)與絕緣膠帶等)所佔空間以及繞線窗沒有利用的空間。線徑越粗,理論上繞線因數越高。鐵氧體的EI或EE型鐵芯更可達0.5,但若考慮安規絕緣與安規沿面距離,依
經驗繞線因數可能只有0.2左右。鐵芯越大,繞線因數也越大,具體的數值,須視鐵芯形狀與大小而定。
以下估算變壓器損耗時,我們先假定鐵心已先選定,參數如下:
- 鐵芯等效面積 Ae
- 繞線窗面積 Wa
- 繞線窗利用率 Winding_factor
- 線圈繞一圈的平均長度 Lmean
- 鐵芯最大磁通密度 Bmax
若要使變壓器銅損能降到最低,則一二次側的線圈最好使用同樣的電流密度,依此原則一二次側分配到的繞線窗比例,與線圈上的均方根電流和圈數乘積成正比。簡單的線圈線組估算如下:


一次側線圈,繞線窗比例為Kwa1,二次側線圈,繞線窗比例為Kwa2,

變壓器銅損損耗的估算更為複雜原因在於,線圈的損耗是取決於Rac,並非Rdc。而Rac受線徑粗細、疊構層和偶合係數的影響,產生的肌膚效應和鄰近效應(proximity
effect),難以用簡單的數學模型估算。為簡化方程式,本文將Rac和Rdc關係,用一個定系數代表(Factor_Rac)。
則變壓器銅損的損耗為:

(9) Transformer core loss:
以flyback轉換器設計,當Krf和Bmax選定時,就可以獲得磁通密度在一個切換週期內swing的範圍,參考鐵芯廠商所附的磁損公式,可推估出變壓器的鐵損。

(Note:Ve為鐵芯的等效體積)
以PC40的材質為例,廠商提供的鐵損公式為:

3. Krf和Vro的選擇,以提昇效率
以上flyback轉換器,在converter部分的功率元件損耗,可以(1)~(9)各別相加,取得最小值,則為可能的效率最佳設計。
下圖以一個45W(30V/1.5A),Vin_dc = 100V離線flyback轉換器為例,代入上述的公式,以Krf和Vro為變數畫出曲線。
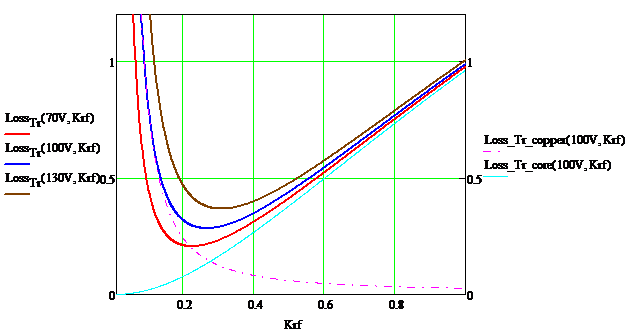
圖六、變壓器損耗與Krf曲線
上圖所示,如果只討論Krf和Vro對變壓器損耗的影響,則Krf的設定會像是在鐵損和銅損上取得平衡點。較小的Vro則是減少了二次側線圈圈數,進而減少了線圈上的銅損。
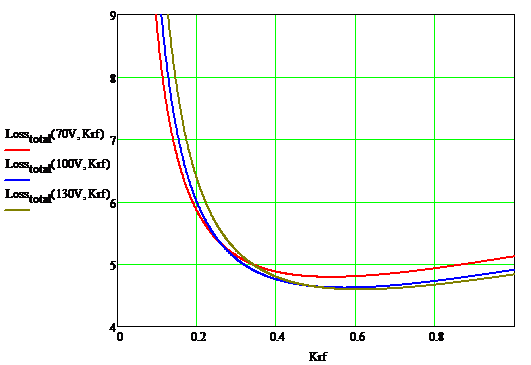
圖七、轉換器整體損耗與曲線
如上圖,很有趣的結果是,Krf界於0.4~0.6之間,可以得到較低的損耗,Vro = 70V並不能得到較佳的效率,反到是Vro
= 100V時最低,這個結果說明了Vro對應一二次側電流所使用的佔空比大小,由於是C.C.M操作模式,一二次側佔空比加起來永遠為一,所以配合了一二次側半導體元件和電容的損耗,一定是一部份少了,另外一半側就會增加,但是還是可以找出一個最佳點。
上圖的曲線是先選定了切換開關晶體,和整流器所得到的結果,事實上Vro如果再往上(>130V 或更高)代表切換開關晶體需選更高的額定電壓,以物理特性而言,Rds_on必定要增加,上面的曲線則不會合用,同理,如果Vro在往下降,則輸出整流器也得換更高的電壓,等效的VF和RD都會增加,對損耗的減少不會有助益。
下面以同樣的方式,代入一個5V/1A PSR的charger,flyback 轉換器操作在D.C.M,作為範例,
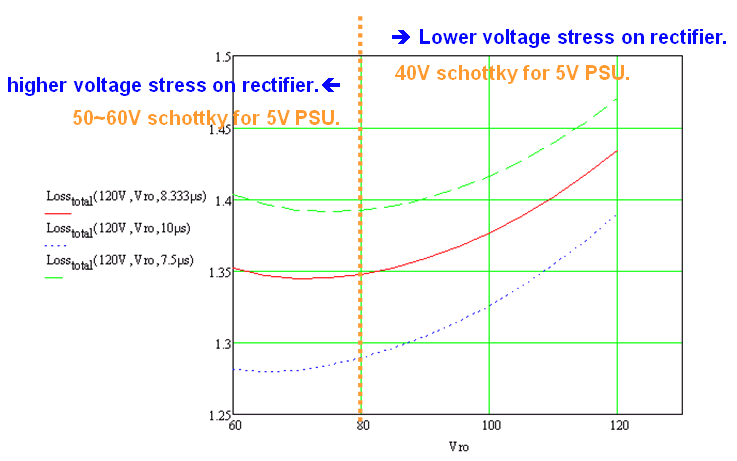
圖八、轉換器整體損耗與 曲線(5V/1A)
在低壓大電流的應用,主要的損耗來自於二次側的整流二極體和輸出電容。所以降低Vro可以提高二次側電流的佔空比,進而降低輸出的均方根電流,減少損耗。在這類的系統應用,反倒是Vro
~70~80V之間可以得到較佳的效率,(但再往下降低,有可能會影響整流二極體的derating)。同時儘量的提高感量,也可以增加佔空比應用率,也降低電流均方根值。
另外提出一點,在變壓器的繞制上常常是不能以相同的電流密度去設計一二次側的線徑的,原因是受限於較佳的偶合系數、降低漏感,線圈往往是要以整層繞滿為基本原則,線徑的選擇不是線性,所以通常的結果,都是選擇在最佳化的左右圈比,然後以降低漏感為先決條件去繞制變壓器。
4. 元件損耗的量測方式
(1) 電容:
電容的ESR是可以直接用impedance analysis分析的。下圖為WAYNE 6500B的量測結果。
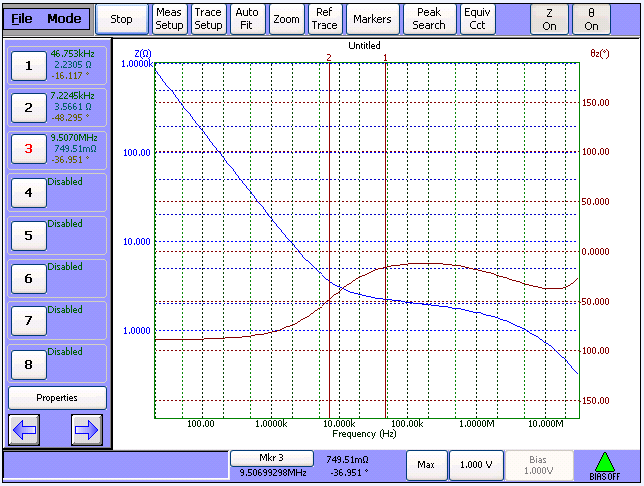
圖九、Impedance of 4.7µF/400V bulk
CAP
此樣品電容可等效為 (Cbulk+ESR) // Rleak的模型。其ESR = 2.23Ω.
量測流入電容的交流電流,則可以直接用current probe量測,或得均方根值,如圖十。

圖十、各個元件的量測方式
輸入輸出電容的損耗,直接由量測到的ESR和交流電流均方根值,直接相乘即可。其中並聯的漏電流阻抗損耗,通常可以忽略不計。
(2) Diode損耗:
其損耗可以用圖十的clamping電路量測,由於現在數位示波器功能強大,可以直接相乘面積獲得損耗。1N4148 clamping的目的是為了讓probe上的寄生電容不會過充,有較快的反應時間,和展示較小的電壓範圍。
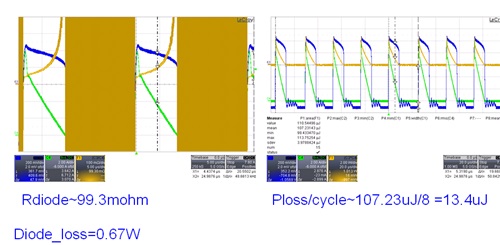
圖十一、Ch3: clamping VD, Ch4: ID, F1=Ch3/Ch4為等效阻抗,F1=Ch3*Ch4則為單一周期損號
(3) BJT or MOSFET Rds_on和損耗:
BJT或者MOSFET Rds_on量測,則可如圖十,用一個高壓MOSFET,箝制住高電位後量測。所量測到的Rds_on乘上電流的均方根值則為晶體元件的導通損耗。
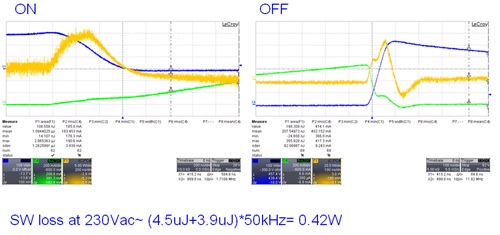
圖十二、Ch3: clamping Vds, Ch4: Ids, Ch3*Ch4為切換損耗
(4) Snubber circuit損耗量測:
如下圖,R1的損耗為Vro,rms2/R1請注意電壓探棒的RTN應接到Vbulk穩定的電壓端。
R2的損耗則為Irms2·R2,使用電流探棒量測R2電流,計算R2的損耗。若直接用電壓探棒量測R2上電壓,則電壓探棒上的寄生電容,也會造成R2多餘的損耗,使得量測失真。同理,二次側的R,C
snubber 電路也可如此量測。

圖十三、snubber circuit損耗量測
參考文獻
[1] 定頻返馳式轉換企設計指南 (王信雄)
[2] 返馳轉換器工作原理 (王信雄)
[3] Optimization Design of Switching Power Supply